이전 챕터에서는 자기회로와 공극에 대해서 이야기했는데 이번에는 전자기적 유도현상에 대해서 이야기하겠습니다. 

전자기적 유도현상은 어릴때부터 꾸준히 배우는 가장 중요한 현상중 하나라고 생각합니다. 대부분의 물리현상은 어떤 현상이 존재하면 그 역의 현상도 존재합니다. 예를 들어 유체속에 중력이 있으면 부력이 작용하는 것처럼 말이죠. 이전에 코일에 흐르는 전류가 주위 공간의 자기장에 변화를 일으킨다는 것을 이야기 했습니다. 반대로 자기장의 변화가 코일의 전류에 영향을 미칩니다. 자석을 코일에 접근시키거나 코일로부터 멀어진다면 코일 안쪽을 지나는 자속에 변화가 생겨 코일에 전류가 흐르는 현상이 나타납니다. 이를 전자기 유도라고 합니다. 

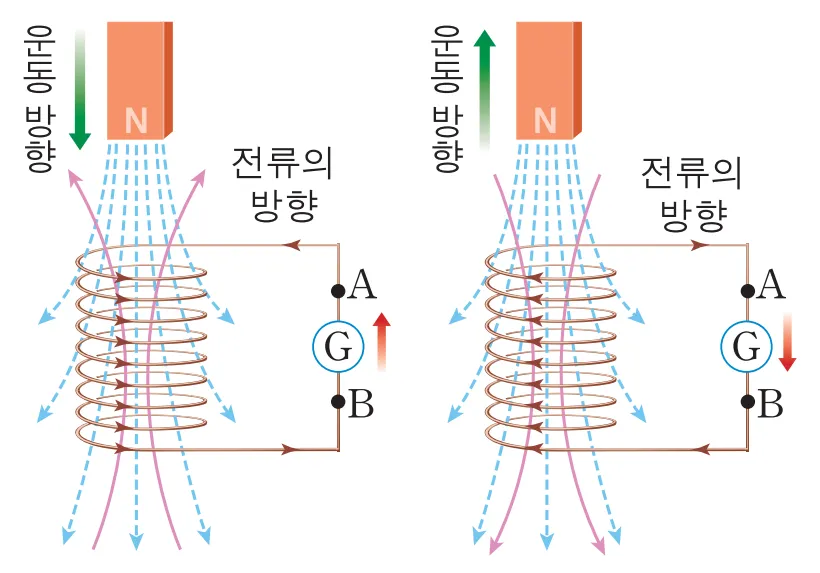
코일에 전류가 흐를 때 방향은 자석의 이동방향에 따라 달라집니다. 왼쪽을 보면 자석의 N극이 코일에 가까워 집니다. 이때는 코일위쪽에서 보았을 때 반시계방향의 전류가 흐릅니다. 그렇게 되면 코일에서 위쪽은 N극 아래쪽은 S극이 되어 다가오는 자석을 방해하는 방향으로 힘이 형성됩니다.  오른쪽 같은 경우는 멀어지는 자석을 막기 위해 위가 S 아래가 N극으로 형성됩니다. 결과적으로 코일 전류는 자석의 움직임을 방해하는 방향의 자속을 만들어낸다고 알 수 있습니다. 이렇게 흐르는 전류가 자속의 변화를 방해하는 쪽으로 작용하는 현상을 렌쯔의 법칙이라고 합니다. 

이때 코일 외부회로를 통해 전류가 흐르는 것은 코일에 기전력이 발생하기 때문입니다. 이를 유도기전력이라고 합니다. 
이때 코일의 자속에 따라 유도기전력의 방향은 렌쯔의 법칙으로 알았는데, 크기는 어떻게 알까요? 바로 패러데이의 법칙으로 알 수 있습니다. 

N은 턴수입니다. 즉 코일의 매 턴마다 자속의 변화율만큼 기전력이 유기되며 직렬로 연결된 N개 턴의 기전력이 모두 더해져 코일 양 단자 사이에 나타남을 알 수 있습니다.  위 식에서 자속은 코일 안쪽을 통과하는 자속을 뜻합니다. 예를 들어 코일 바깥쪽을 흐르는 자속이 있다면 이는 식과 전혀상관없습니다.  턴수 N인 코일에서 코일 내부를 지나는 자속 쇄교량 혹은 쇄교 자속을

다음과 같이 정의할 수 있습니다.  

위 패러데이 법칙 또한 쇄교자속을 이용하면

다음과 같이 정의할 수 있습니다. 즉, 코일 양단에 나타나는 기전력은 쇄교자속의 변화율과 같은 걸 알 수 있습니다. 

지금까지 외부에서 자속의 변화가 생길 떄 코일에 기전력이 유기되는 것을 알았는데요, 이번에는 코일 자체에서 전류가 변화할 때 자속의 변화를 알아보겠습니다. 

전류가 증가하거나 전류가 감소한다면 자속은 변합니다. 예를 들어 위와 같은 그림인데 자석을 보지 않겠습니다.

이떄, 자석이 없다고 가정하고 코일 내부에 철심이 있다고 가정하면, 전류의 세기가 변할 시 철심에 자속의 양은 달라지게 됩니다. 전류가 커지면서 자속이 증가한다면 방해하는 방향으로 기전력이 유기됩니다. 즉 자속을 방해하기 위한 기전력이 유기되어 전류의 상승을 억제하려고 합니다. 

쇄교자속을 다음과 같이 쓸 수 있다는 걸 압니다. 이때 맨 오른쪽 i 에 붙어있는 식을 L이라는 인덕턴스라고 정의합니다. (단위는 H) 인덕턴스가 뭐냐? 라고 묻는다면 쇄교자속과 전류사이의 비례상수 라고 이야기할 수 있습니다. 

전기공학을 공부하는 학생은 알겠지만 회로에서 인덕터에서 사용되는 인덕턴스와 같은 인덕턴스입니다. 기전력의 관점에서 다시 정리하면 

다음과 같이 됩니다. 회로 관점에서 보면 코일에 전류가 흐를 때 코일 양단에 어떤 기전력이 나타나는 지 특성을 표현하는 상수가 됩니다. 인덕턴스는 주어진 전류로 얼마나 많은 자속쇄교량이 만들어지는 지를 나타냅니다.  코일의 인덕턴스가 크다는 것은 작은 전류로 큰 자속이 만들어진다는 뜻이고 이는 자기저항이 작다는 것과 같습니다. 코일에 자기저항이 작은 강자성체 철심을 사용하면 철심이 없을 때에 비해 인덕턴스가 몇천배 증가할 수 있겠죠. 

오늘 개념이 많이 나왔는데 인덕턴스와 유도기전력 개념은 알고가셨으면 좋겠습니다. 인덕턴스는 전기전자공학에서 단순히 전기기기 뿐만 아니라 전자회로, 교류회로 등 다양한 곳에서 사용되는 개념입니다. 

다음에는 자기 인덕턴스, 상호 인덕턴스와 교류전압과 자속에 대해 이야기 하겠습니다.

 이전 챕터에서는 투자율과 자화특성곡선에 대해서 이야기했는데 이번에는 자기회로와 공극에 대해서 이야기하겠습니다. 

코일에서 만들어진 자속은 코일의 한쪽에서 나와 경로를 거쳐 코일 반대편으로 되돌아 옵니다. 자기력선이 폐루프를 그리기 때문에 코일에서 나간 자속과 들어온 자속은 같습니다. 즉, 전기회로처럼 자기력선 역시 회로와 비슷한 방식으로 작동합니다. 따라서 이를 마치 자기회로 방식으로 해석할 수 있습니다. 저희가 이전 챕터에서 자기저항이라는 것을 이야기했는데 기자력이 전압처럼 자기저항이 전기저항처럼 그리고 자속이 전류처럼 대응된다는 것을 알 수 있습니다. 전기회로와 다르게 자기회로에서는 누설자속이라는 것이 존재합니다. 도체의 도전율이 부도체의 10^15배 정도 차이나는 반면 강자성체의 투자율은 비자성체의 겨우 수천배밖에 되지 않습니다. 이에, 자속이 누설되는 누설자속 현상이 발생합니다. 자기회로 방식은 전기회로처럼 저항의 합같은 방식으로 직렬 병렬을 계산할 수 있다는 편리성이 있습니다. 

한편 자기저항이 투자율*면적의 역수라는 사실을 배웠는데, 공기중에서 자기저항이 철심에서 자기저항보다 훨씬 높다는 것을 저번 게시글에서 이야기 했습니다. 아래 그림을 보면 다음과 같이 공기로 이루어진 간격인 공극이 존재합니다. 공극에서는 자기저항이 철심보다 훨씬 높기 때문에 기자력 강하 ( 전기회로로 따지면 전압강하) 가 훨씬 크게 나타납니다. 한편, 저희는 자화특성곡성에서 투자율이 동작점에 따라 관계가 일정하지 않다는 것을 알고 있습니다. 이에, B와 H의 상태를 모를경우 비선형적인 함수로 인해 수치해석적 방법을 이용합니다. 

지금까지 자기회로, 공극에 공부했습니다. 다음에는 전자기적 유도현상에 대해 이야기 하겠습니다. 

 이전 챕터에서는 자구와 자기포화에 대해서 이야기했는데 이번에는 투자율과 자화특성에 대해서 이야기하겠습니다. 

같은 재료의 철심에 같은 기자력을 가하였다 해도 철심의 크기와 형상에 따라 자속의 양이 달라집니다. 예를 들어 같은 턴수에서 철심의 길이를 짧게 만들어 준다면 코일이 조밀해지면서 자속이 커집니다. 즉 철심의 길이에 따라 철심을 자화시키는 힘이 달라지므로 단위길이당 기자력을 정의할 필요가 생깁니다. 이를 H 자계강도라고 하고 자기장의 세기라고도 합니다.

철심 재료가 얼마나 자화가 잘 되는 성질을 지녔는지는 코일의 총 기자력과 총 자속 전체적으로 비교하는 것보다 각각 자구에 가해지는 기자력과 각각의 자구가 어느정도만큼 자화되었는지의 관계로 표현해야합니다. 그래야 철심의 형상에 관계없이 철심이 가진 고유의 자화특성을 알 수 있으니깐요. 그렇기 때문에 H 자계강도와 B 자속 밀도의 관계로 투자율을 정의합니다.  

투자율이 클수록 자화가 쉽게 이루어지며 같은 기자력에서 더 많은 자속을 만들어 냅니다. 빈 공간에서 투자율은 상수로 정해져있습니다. 중요한 숫자라 외워놓는게 좋습니다. 

이를 기준으로 어떤 철심 재료의 투자율이 공기중의 투자율의 몇배인지 나타낸 것을 비투자율이라고 합니다. 즉 

비투자율은 다음과 같이 나타낼 수 있고, 주로 철심의 비투자율은 3000정도로 생각하면 됩니다. 

전에 자기저항과 관련된 식을 보았는데 이제 자계강도를 이용해 자기저항을 다른 방식으로 나타낼 수 있습니다. 

자기저항 즉, reluctunce 식을 정리해보면 위 그림의 오른쪽 처럼 정리가 됩니다. 이는 전기에서 저항이 가지는 관계와 비슷하다는 걸 알 수 있습니다. 즉 전기저항이 굵고 짧은 도체의 저항이 작듯, 굵고 짧은 철심은 자기저항이 작게 됩니다. 

또한 전기에서 저항계산처럼 자기저항 역시 병렬, 직렬 회로로 분석이 가능합니다. 

자화특성곡선은 자계강도와 자속밀도사이의 관계를 그래프로 나타낸 것입니다. 

저번 게시글에서 보여주었던 자속과 기자력 그래프와 매우 유사합니다. 자화특성곡선은 해당 자성재료의 자화특성을 아는데 굉장히 중요합니다. 저 역시 인턴생활때 자화특성곡선을 숱하게 보았습니다. 우수한 자기적 특성이란 선형영역에서 투자율이 크고 최대로 얻을 수 있는 자속밀도, 즉 자기포화에 이르렀을 때의 자속밀도인 포화자속밀도가 큰 것을 말합니다. 자화특성곡선을 통해 해당 자기적특성을 고려해야하고 전기적, 기계적 특징도 고려해야할 요소입니다. 

자화특성곡선은 후에 히스테리시스 곡선부터 여러가지로 전기기기에서 필수적인 요소입니다. 또한 투자율 자계강도를 정확하게 알고 넘어가야 추후 설명에서 어려움이 없을거라 예상됩니다. 다음시간에는 자기회로와 공극, 전자기유도현상을 알아보겠습니다. 

이전 챕터 에서는 자기장과 기자력, 자기저항에 대해서 이야기했는데 이번에는 자기저항과 자화에 대해서 이야기하겠습니다. 

자화가 잘 되는 물질이 있고 그렇지 못한 물질이 있다는 사실을 알고 있습니다. 자기장에 민감하게 반응하는 성질을 가진 물체를 강자성체라고 부르고 흔히 철, 코발트, 니켈등이 있습니다.

더 자세하게 들어가면 강자성 물질의 원자들은 전자의 스핀에서 비롯된 각자의 자기장을 지니고 있습니다. 자기장의 상호작용으로 인근 원자들 사이의 전자스핀 방향을 서로 일치시키려는 힘이 작용하고 이게 점점 확장을 거듭하여 결과적으로 특정 부분의 원자들이 같은 방향의 스핀을 지닌 하나의 집단을 이루게 됩니다. 이런 집단적 동화작용이 여러 구역마다 이뤄지기 때문에 이런 구역을 자기구역 즉 magnetic domain 이라고 하며 자구로 나뉘게 됩니다. 이때, 외부에서 모든 자구에 공통의 자기장이 가해진다면, 강자성체의 자구들이 외부 자기장의 방향으로 나란히 정렬하는 작용이 일어나 전체적으로 같은 자기장이 되고 자석처럼 정렬됩니다. 이를 자화라고 합니다. 

자화시키는 방식은 강자성체에 코일을 감아 전류를 흐르는 방법도 있습니다. 어쨌거나 이와 같은 방식도 자기장을 형성하므로 강자성체가 같은 방향으로 자화됩니다. 강자성체는 마치 자석처럼 되며, 코일이 기존의 갖던 자속보다 훨씬 큰 자속이  형성됨을 알 수 있습니다. 코일에 삽입하는 물체를 자심이라고 하며 보통 철성분이기에 철심이라고 합니다. 

철심을 자석으로 만드는 자화전류는 코일에 흐르는 전류를 뜻합니다. 결과적으로 코일의 조그만 전류가 코일의 자구들을 정렬시켜 자화시키는 것이라고 할 수 있습니다. 

자기포화

철심이 자화되는 정도는 외부 자기장의 세기에 따라 달라집니다. 외부자기장이 강할수록 자구들의 정렬도가 높아지며 자속이 증가하는데 철심안에 있는 자구들이 다 정렬한다고 하면 더이상 자속이 증가하지 않습니다. 이를 포화되었다고 합니다. 그럼 이제 그래프를 보겠습니다. 

철심이 있을 때를 보겠습니다. 철심이 있을 경우

기자력에 비례해서 선형적으로 증가하다 해당 강자성체의 자구들이 전부 자화되면 포화영역에 들어오게 됩니다. 자속의 변화율은 급속도로 줄게 됩니다. 이때, x축이 기자력, y축이 자속이므로 기울기는 자기저항의 역수가 된다는 것을 알 수 있습니다. 기울기 관점에서 보면, 처음에는 자기저항이 작다가 점점 커지는 것을 알 수 있겠네요. 철심이 없을 때를 보자면, 철심이 없는 경우 유의미한 변화가 없습니다. 이는 강자성체를 사용하지 않았기 떄문이겠죠 

코일에 흐를 수 있는 최대 전류는 도체의 단면적에 비례하고 코일의 턴수는 도체의 길이에 비례합니다. 이 말은 결국 코일이 제공할 수 있는 최대기자력은 코일에 사용된 도체의 체적에 비례한다는 뜻입니다. 효율적으로 이용하기 위해서는, 철심을 자기포화 직전까지 자화시켰을 때가 철심의 이용효율이 최대화 됩니다. 이에 대부분의 전기기기는 철심이 경계영역까지 자화되는 범위에서 동작하게 만들어집니다. 

지금까지 기자력 자속 곡선, 자화, 철심, 자구등에 공부했습니다. 모두 습득하고 가야 그 다음 챕터들을 이해할 수 있습니다. 다음 내용에는 투자율과 자화특성곡선 자기회로 공극등에 대해 이야기하겠습니다.